New Mexico Tech
Earth and Environmental Science

ERTH 455 / GEOP 555 - Geodetic Methods

Lab 13: Volcano Deformation

Note that you DO NOT have to work on redoubt today!

Introduction

Today you will use some co-eruptive displacements from Redoubt volcano's 2009 eruption and hopefully learn a bit about its source. You will do 2 things: (1) implement the Mogi model, (2) find the best source parameters given the displacements.

Caveats:

(1) I've already shown that the Mogi source isn't the best model for the co-eruptive phase. We'll use it anyway for the data, because it's a simple model, and we're here to learn the methods.

(2) The method I'll have you implement to solve for the non-linear parts is inefficient and imprecise. Again, it's one way to gain an intuition to find solutions to these problems; you should embark on a journey to learn about the many efficient non-linear methods / solvers that are out there yourself; often they take a parameter range in which they do their magic, which reduces to a single function call. Not much to be learned in a lab.

I bring up these points, to make sure you don't assume the methods used here are the ones you should use for the rest of your career; far from it! They're a starting point.

The Forward Model

First, start out with implementing a function [dr, dz] = mogi(x,y,d,C), which given a set of distances (x,y) in carthesian coordinates away from a source location, a source depth d and a source strength C returns radial and horizontal displacements at these points.

You can test your model with these values:

>> [dr, dz] = mogi([1000, -1000, 2000, 0]', [1000, -1000, 2000, 0]', 17000, (0.75*0.05*1000^3)/pi)

dr =

   0.003400610640462
   0.003400610640462
   0.006596168094920
                   0


dz =

   0.040878112348779
   0.040878112348779
   0.039645659112996
   0.041303185923502			
		

The x,y distances are in meters away from a source at 17 km depth that changes in volume by 0.05 km3. What are the units of dr, dz?

The ``Inverse'' Model

Download the file invert_mogi_incomplete.m. It contains a matrix displacements; its contents is described in the comments and a vector volcano which contains in UTM coordinates (meters) the location of the volcano.

Write a script that searches within +/-10 km of the volcano's location, within a depth range of, say 40 km for a Mogi source. Note that the Mogi model is non-linear with respect to location and hence you'll need to come up with a non-linear solution scheme. I'd recommend you do a grid search in 1km intervals through your model domain. You can invert for your source strength C using least-squares; the model is linear in that parameter.

Note that this is not the best way to solve this problem, but it provides considerable intuition as to what more sophisticated methods might be after.

Hints

A few things you need to to:

• setup your data vector concatenating ur, uz in correct units
• write loops to iterate over x, y, depth
• turn your global coordinates of the stations to radial distances with respect to the suspected source location (x,y)
• set up your design matrix (G) to solve for C in the innermost loop (depends on r, d)
• invert for C - the source strength
• compute the forward model using the mogi function you've written before
• calculate the norm of the residual vector (use function norm in Matlab)
• if your new norm is better than any of the previous norms, save your current model parameters in variables, say, best_x, best_y, best_d, best_C, current_resid_norm
• at the beginning of your script set current_resid_norm=inf

What is the expected source depth and the volume change of the magma reservoir (convert!)? Give these values in sensible units.

Plotting (optional)

If you feel so inclined, on redoubt under /data/GEOP555/lab13/redoubt_gmt.zip is a zipfile will all the ingredients you need to make the plot below. You can forward model the expected displacements and convert the observed data and modeled data from cylindrical to cartesian coordinates and add them to the plot with psvelo.

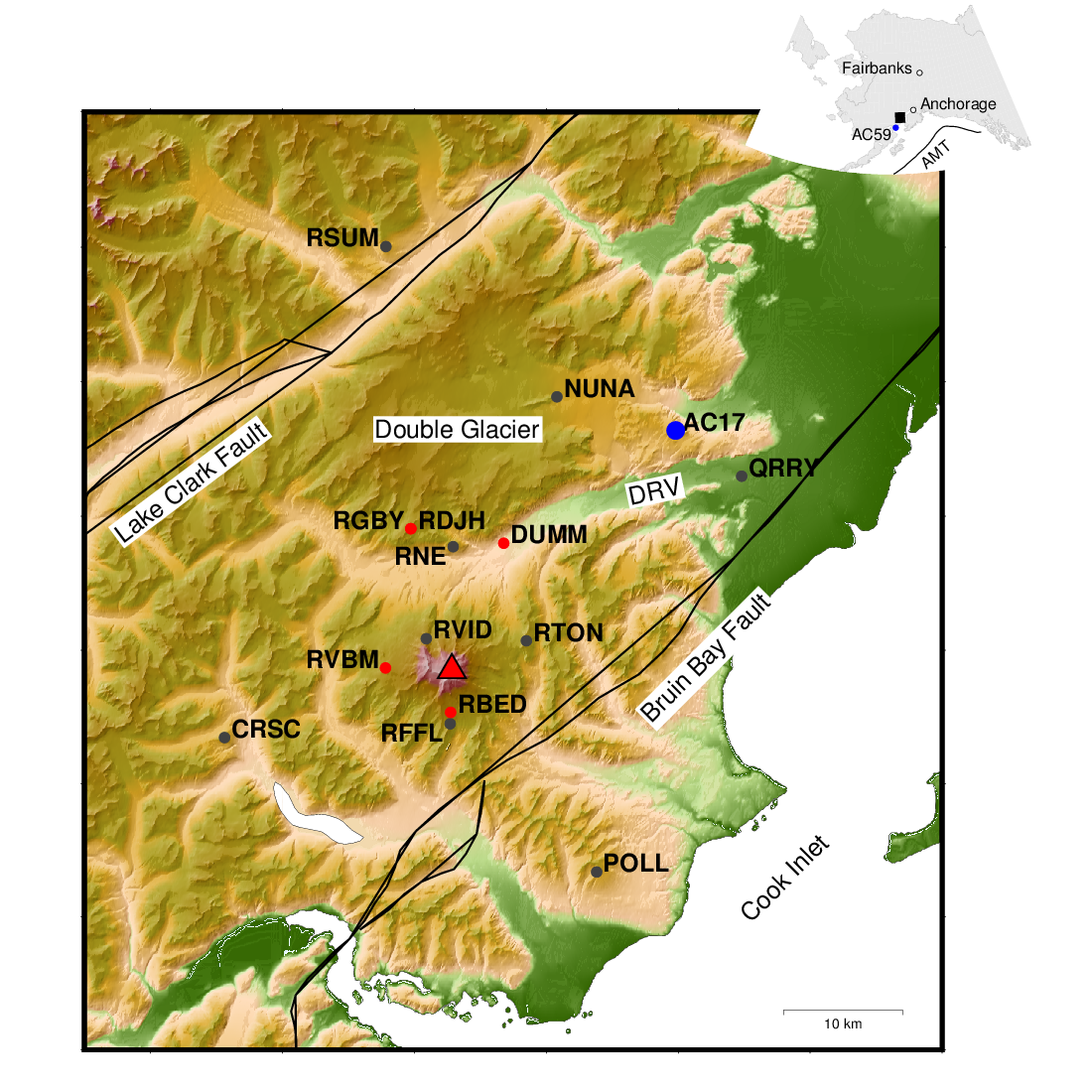
Deliverables: (submit via canvas in a zip file!)

• mogi function file
• inverse_mogi script
• separate document with answers to questions in bold (preferably a PDF)
• (optional) Map with data and displacements modeled with the best fitting source parameters